Single-crystal Silicon is an uninterrupted lattice of Si atoms comprising a semiconducting solid. Polycrystaline Silicon (aka “poly”) is a random assembly of crystal grains which act as a resistive material. In micro- or nano-scale geometries, poly-Si behaves like a conductor. Today, most electronic devices are made by manipulating pure Si and/or poly-Si. There are other semiconducting materials in use besides Si, but the basic principles are mostly the same, so for now we’ll limit our attention to Si-based devices.
Single-crystal Si comes in two forms:
Intrinsic — the lattice contains only Si molecules.
Extrinsic — a Si lattice with periodic insertion of dopant molecules.
In all types of materials, the mobile charge density is governed by the mass action law, which dictates that the product of mobile \(e^-\) and \(h^+\) concentrations should be constant. The intrinsic carrier concentration, \(n_i\), is the \(e^-\) concentration of an intrinsic material in a state of thermal equilibrium. At equilibrium, we expect equal concentrations of \(e^-\) and \(h^+\), so \(p_i=n_i\).
In an extrinsic material, the charge balance is disturbed so that \(p\neq n\). Their product remains constant:
\[n\times p = n_i \times p_i = n_i^2.\]
A value for \(n_i\) is solved using the solutions from energy band theory:
\[\begin{aligned} n\,p &= n_i^2\\ \textrm{where~} n_i &= \sqrt{N_C\,N_V}\exp\left(-\frac{E_C-E_V}{2k_BT}\right)\\ &= \sqrt{N_C\,N_V}\exp\left(\frac{-E_g}{2k_BT}\right)\end{aligned}\]
This result allows us to conveniently determine carrier concentrations without precisely knowing the material’s Fermi level.
Random mobile charges are generated by heat energy. In an intrinsic material, the \(e^-\) and \(h^+\) charges exist in equal numbers. Extrinsic material is doped with one of two types of impurities:
Donors — have one excess \(e^-\) in the valence shell (i.e. five total), so they donate one surplus mobile \(e^-\) to the material, but leave behind one immobile \(h^+\) at the lattice point where the dopant atom resides.
Acceptors — have one too few valence \(e^-\) (i.e. there are three total), so they tend to “steal” or accept a mobile \(e^-\) from the surrounding material, leaving a mobile \(h^+\) in the material, and a fixed \(e^-\) at the dopant site.
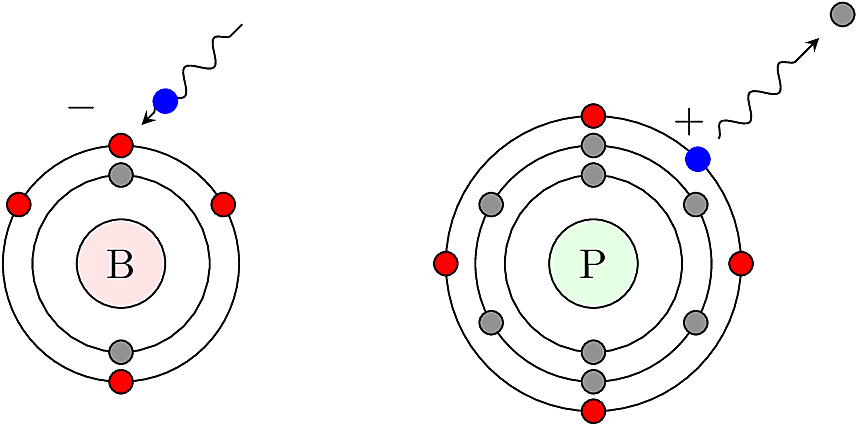
To make complete covalent bonds with Si neighbors, and to satisfy the octet rule, an acceptor (e.g. Boron) steals a mobile \(e^-\) to achieve a valence shell of four, leaving behind a mobile \(h^+\). Conversely, a donor (e.g. Phosphorus) donates a mobile \(e^-\), leaving behind a fixed \(h^+\) at the donor site.

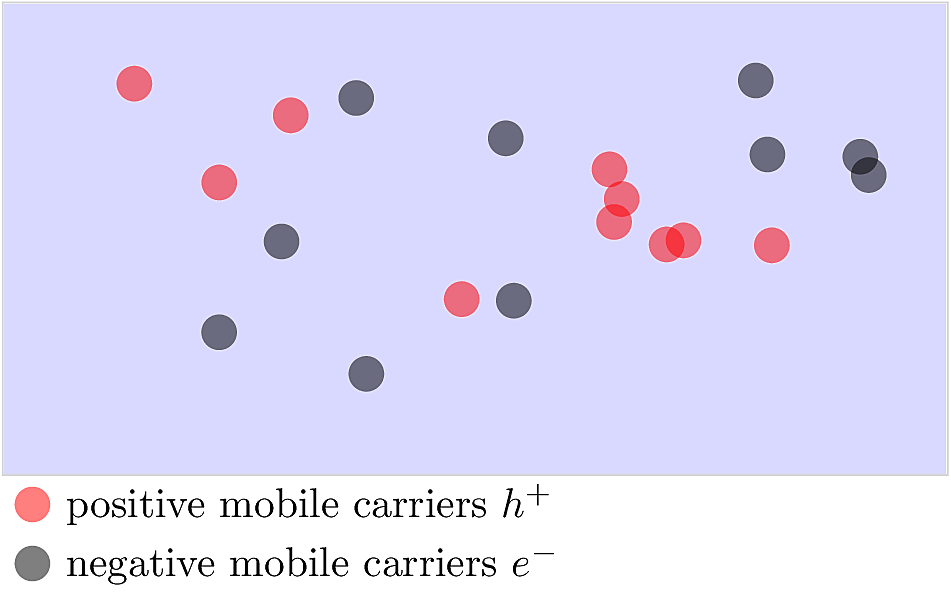
In an intrinsic material, thermal energy excites an equal density of mobile \(e^-\) and \(h^+\) as shown below. At thermal equilibrium, the material is charge-neutral, meaning the total positive charge balances the total negative charge.
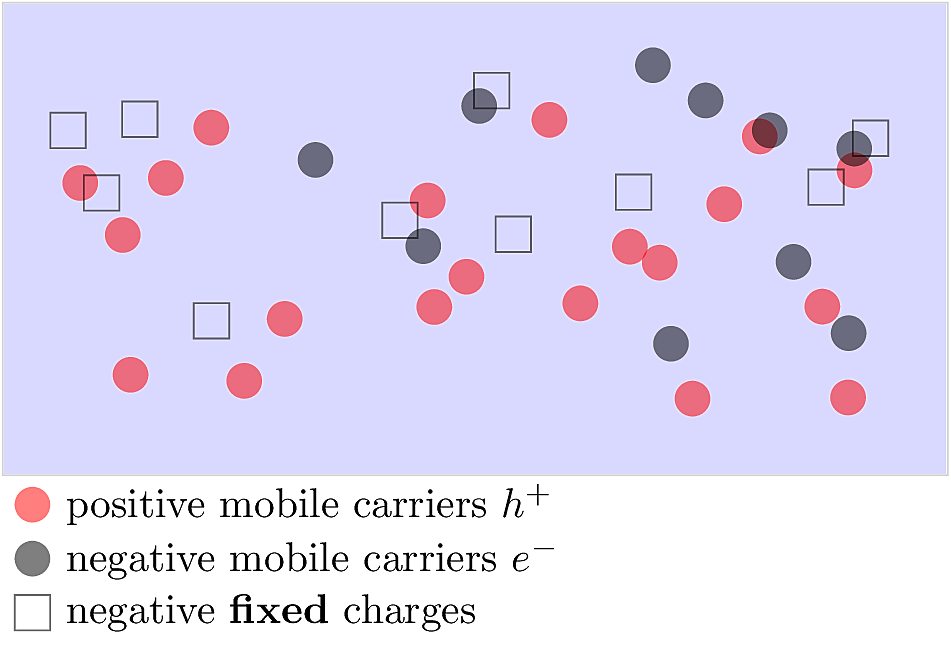
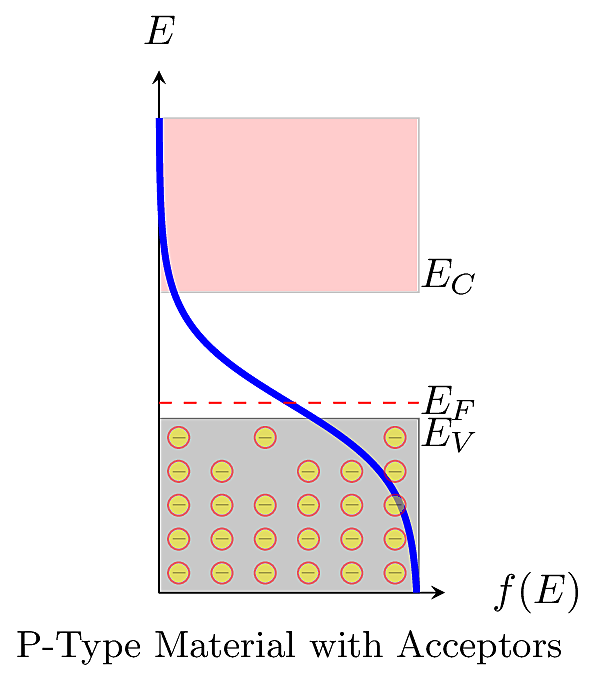
In a P-type extrinsic material, acceptor dopants contribute a surplus of mobile \(h^+\). Each acceptor atom retains an immobile negative charge stuck to its valence shell. At thermal equilibrium, the total negative charge should balance the total positive charge, so the fixed negative charges suppress the number of mobile \(e^-\). If the material is doped with a large acceptor density of \(N_A\) dopants per \(\,\text{cm}^3\), such that \(N_A\gg n_i\), then the mobile \(h^+\) concentration is \(p\approx N_A\) carriers per \(\,\text{cm}^3\). By the mass action law, we have:
\[\begin{aligned} np &= n_i^2\\ p &\approx N_A\\ \Rightarrow n &\approx \frac{n_i^2}{N_A}\end{aligned}\]
The figure below illustrates the distribution of mobile and immobile charges in a P-type material.
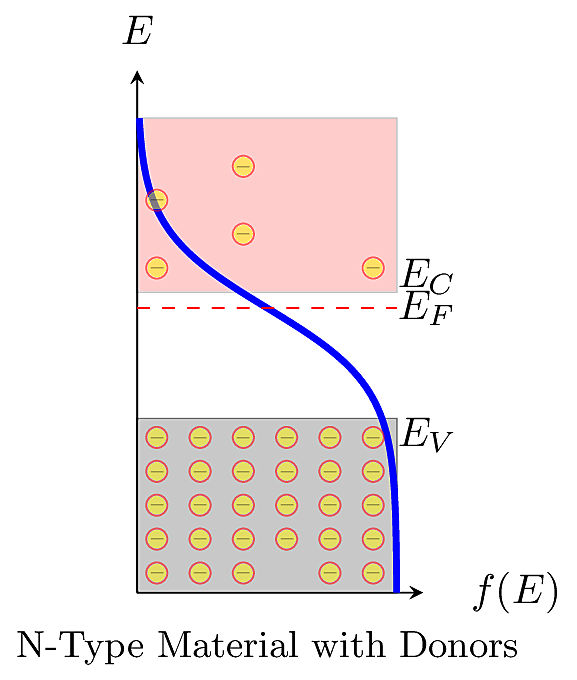
A material doped with donor atoms is said to be N-type, because it will contain a surplus of mobile \(e^-\), with a reduced density of mobile \(h^+\). Each donor atom contributes an immobile positive charge. If the material is doped with a large donor density of \(N_D\) dopants per \(\,\text{cm}^3\), such that \(N_D\gg n_i\), then the mobile \(h^+\) concentration is \(n\approx N_D\) carriers per \(\,\text{cm}^3\). By the mass action law, we have:
\[\begin{aligned} np &= n_i^2\\ n &\approx N_D\\ \Rightarrow p &\approx \frac{n_i^2}{N_D}\end{aligned}\]
A material can be doped with a mixture of acceptor and donor atoms. In this situation, usually one dopant species is dominant. If \(N_A\gg N_D\), then the material is effectively P-type. If \(N_D\gg N_A\) then the material is effectively N-type.
Doping alters the balance of mobile carriers in a semiconductor. This means that the statistical distribution of electron energies is changed, and there is consequently a shift in the material’s Fermi level \(E_F\). In an undoped semiconductor, the intrinsic Fermi level \(E_i\) is roughly halfway between the conduction band and valence band edges. When the material’s Fermi level is disturbed by doping, the mobile carrier densities are related to the change in the Fermi level as follows:
\[\begin{aligned} n &= n_i\exp\left(\frac{E_F-E_i}{kT}\right)\\ p &= n_i\exp\left(\frac{E_i-E_F}{kT}\right)\end{aligned}\]
So when there are more mobile \(e^-\), it increases the negative carrier concentration \(n\), so \(E_F > E_i\). In other words, the Fermi level is shifted toward the conduction band as shown below.
Similarly when there are more mobile \(h^+\), it increases the positive carrier concentration \(p\), so \(E_F < E_i\). In other words, the Fermi level is shifted toward the valence band as shown below.
For typical doped semiconductors, where the doping concentration is much greater than \(n_i\), the Fermi level is predicted by a simple approximation:
\[\begin{aligned} \text{(N-type)~} E_F &= E_i + kT\ln \left(\frac{N_D}{n_i}\right)\\ \text{(P-type)~} E_F &= E_i - kT\ln \left(\frac{N_A}{n_i}\right)\end{aligned}\]
These equations underpin the operation of most semiconductor devices.